More technical details on Dwave System’s Quantum Computing

by

D-Wave Senior Scientist and condensed matter physicist Mohammad Amin gave a highly technical presentation at MIT. (54 slides in this power point presentation) Dwave recently demonstrated a 28 qubit computer. They are predicting that they will have 512 qubit and 1024 qubit quantum computer systems in 2008. If Dwave is successful then in 2009 it will begin to greatly accelerate the development of molecular nanotechnology which needs better molecular modeling.

adiabatic quantum computer required conditions
Adiabatic quantum computer (AQC) required conditions

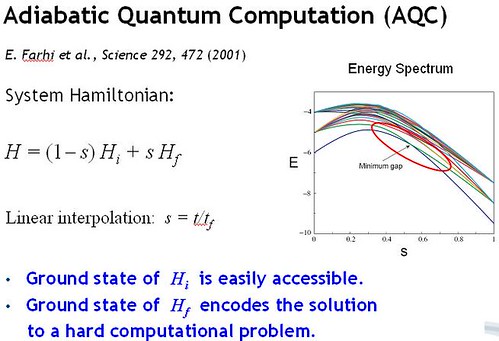
Theory from 2001 requires an energy gap
AQC Theory from 2001 requires an energy gap

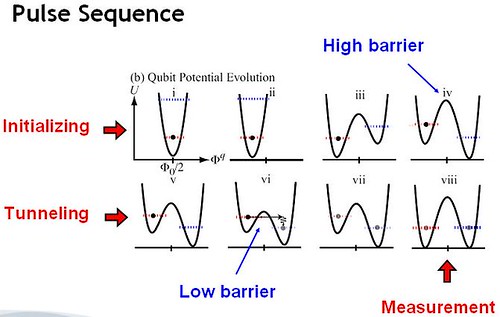
Theory predicts energy levels
AQC Theory predicts energy levels

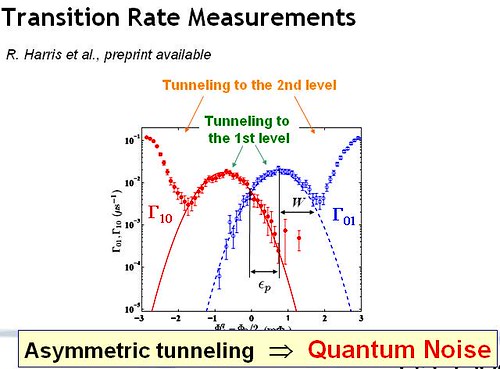
Experimental measurements show energy levels consistent with quantum noise
Experimental measurements show energy levels consistent with quantum noise

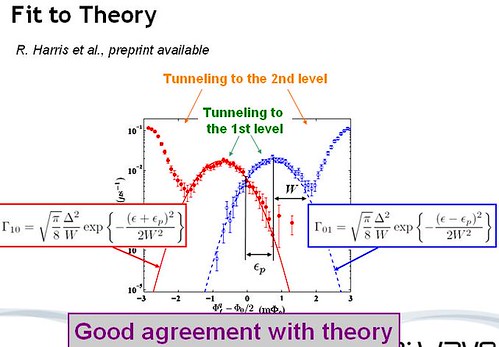
Experimental measurements fit the theory
Experimental measurements fit the theory

What the difference regions of quantum effects, mixed effects and classical effects would be
What the difference regions of quantum effects, mixed effects and classical effects would be


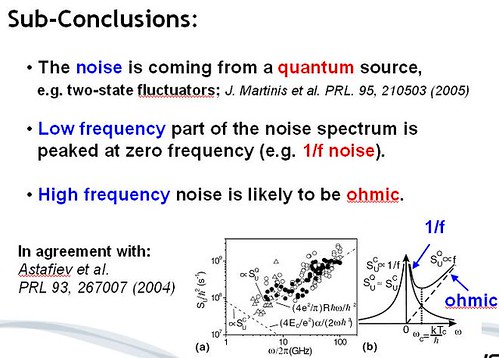
Interpreting several Measurements

the experimental results are indicating that Dwave is looking at quantum results
The experimental results are indicating that Dwave is looking at quantum results

FURTHER READING
The point of view of Dwave skeptic Scott Aaronson

Amin and Berkley maintained that their 16-qubit device was indeed a quantum computer and their evidence was that simulations of its behavior that took quantum mechanics into account gave, they said, a better fit to the data than simulations that didn’t. On the other hand, they said they were not able to test directly for the presence of any quantum effect such as entanglement. (They agreed that entanglement was a non-negotiable requirement for quantum computing.)

Dwave CTO Geordie Rose replies in the comments

Finally, the variety of demos we’ve run (including sudoku, image matching, etc.) are not “crap”. They use a novel hybrid approach to integrating QCs into classical solvers. In hindsight it is pretty obvious that to make any QC useful it needs to be integrated with the best known classical techniques regardless of what quantum algorithm it’s embodying. And while I’ve said this 10^87 times I’ll say it again: what we’re doing is explicitly heuristic and has no global optimality guarantees. While you can use the system we’re building on decision problems it is natively an optimization solver for quadratic unconstrained binary optimization problems

From another commenter:

How then does Dwave “solve” the image feature matching problem using just 28 bits, for images that are large and have many features (such as those that Dwave used in their SC demo)? Apparently they “cheat” and break the overall problem into many small maximum common subgraph problems (of a size that can be encoded in 28 bits). Each small MCS problem is “solved” on the QC, and then the solutions are somehow combined classically.

Like the soduku, solve the 3X3 squares iteravely then combine to a 9X9 solution.

It is not a cheat in that they are using the quantum system to its best ability by combining with our current best methods. To only solve problems with quantum systems is like having only allowing pencil and paper on tests when the real world has regular computers, wikipedia and Google.