Theory of High-TC Superconductivity: Accurate Predictions of TC
The superconducting transition temperatures of high-TC compounds based on copper, iron, ruthenium and certain organic molecules are discovered to be dependent on bond lengths, ionic valences, and Coulomb coupling between electronic bands in adjacent, spatially separated layers.1 Optimal transition temperature, denoted as TC0, is given by the universal expression kBTC0 = [formula] is the spacing between interacting charges within the layers, ζ is the distance between interacting layers and [ ] is a universal constant, equal to about twice the reduced electron Compton wavelength (suggesting that Compton scattering plays a role in pairing). Non-optimum compounds in which sample degradation is evident typically exhibit TC less than TC0. For the 31+ optimum compounds tested, the theoretical and experimental TC0 agree statistically to within plus or minus 1.4 K. The elemental high TC building block comprises two adjacent and spatially separated charge layers; the factor arises from Coulomb forces between them. The theoretical charge structure representing a room-temperature superconductor is also presented.
The Columb force theory accurately predicts the critical temperatures of a lot of known superconductors and it predicts that room temperature superconductors are possible.
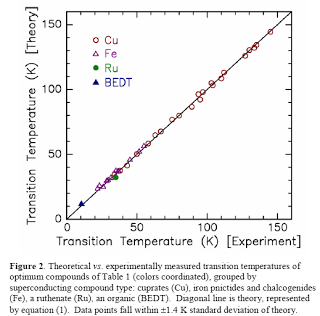
1. The theory accurately predicts TC0 for the 36 optimal high-TC superconductors of Table 1, as illustrated in the distribution of errors shown in Figure 6. The mean error between theory and experiment is 1.4 K.
2. The minimum superconducting structure contains full Type I and Type II charge reservoirs .
3. A conducting charge sheet is non-superconducting without a second mediating charge layer next to it.
4. Experimental validations of ℓ have been obtained for three cuprates and an organic from measurements of London penetration depths and Hall coefficients, yielding an effective mass m* 1.5 m0 and m* independence of TC0. The length ℓ has been verified for the iron-chalcogenide K0.8Fe1.7Se2 from measurements of Fermi wave vector kF by ARPES .
5. The limit portends a room temperature superconductor, as equation (1) evaluates to TC0 = 331 K .
6. TC0 is proportional to the root-mean-square average of indirect (interlayer) Coulomb forces
If you liked this article, please give it a quick review on ycombinator or StumbleUpon. Thanks

Brian Wang is a Futurist Thought Leader and a popular Science blogger with 1 million readers per month. His blog Nextbigfuture.com is ranked #1 Science News Blog. It covers many disruptive technology and trends including Space, Robotics, Artificial Intelligence, Medicine, Anti-aging Biotechnology, and Nanotechnology.
Known for identifying cutting edge technologies, he is currently a Co-Founder of a startup and fundraiser for high potential early-stage companies. He is the Head of Research for Allocations for deep technology investments and an Angel Investor at Space Angels.
A frequent speaker at corporations, he has been a TEDx speaker, a Singularity University speaker and guest at numerous interviews for radio and podcasts. He is open to public speaking and advising engagements.