For the first time, physicists have performed machine learning on a photonic quantum computer, demonstrating that quantum computers may be able to exponentially speed up the rate at which certain machine learning tasks are performed—in some cases, reducing the time from hundreds of thousands of years to mere seconds. The new method takes advantage of quantum entanglement, in which two or more objects are so strongly related that paradoxical effects often arise since a measurement on one object instantaneously affects the other. Here, quantum entanglement provides a very fast way to classify vectors into one of two categories, a task that is at the core of machine learning.
In the future, the researchers hope to scale the method to larger numbers of qubits. They explain that higher-dimensional quantum states can be encoded using a photon’s degree of freedom of orbital angular momentum, or by using other properties.
“We are working on controlling an increasingly large number of quantum bits for more powerful quantum machine learning,” Lu said. “By controlling multiple degrees of freedom of a single photon, we aim to generate 6-photon, 18-qubit entanglement in the near future. Using semiconductor quantum dots, we are trying to build a solid-state platform for approximately 20-photon entanglement in about five years. With the enhanced ability in quantum control, we will perform more complicated quantum artificial intelligence tasks.”
Machine learning, a branch of artificial intelligence, learns from previous experience to optimize performance, which is ubiquitous in various fields such as computer sciences, financial analysis, robotics, and bioinformatics. A challenge is that machine learning with the rapidly growing “big data” could become intractable for classical computers. Recently, quantum machine learning algorithms were proposed which could offer an exponential speedup over classical algorithms. Here, we report the first experimental entanglement-based classification of two-, four-, and eight-dimensional vectors to different clusters using a small-scale photonic quantum computer, which are then used to implement supervised and unsupervised machine learning. The results demonstrate the working principle of using quantum computers to manipulate and classify high-dimensional vectors, the core mathematical routine in machine learning. The method can, in principle, be scaled to larger numbers of qubits, and may provide a new route to accelerate machine learning.
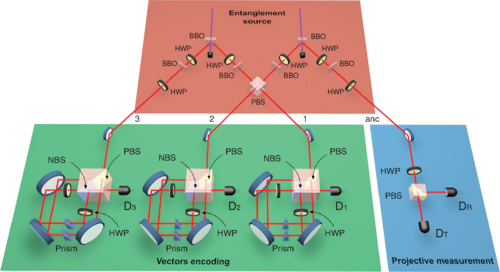
Experimental setup for quantum machine learning with photonic qubits. Ultraviolet laser pulses with a central wavelength of 394 nm, pulse duration of 120 fs, and a repetition rate of 76 MHz pass through two type-II β-barium borate (BBO) crystals with a thickness of 2 mm to produce two entangled photon pairs
Scott Aaronson on the Harrow, Hassidim, Lloyd Machine Learning Quantum Algorithm
Scott Aaronson has a 4 pager on the machine learning mini-revolution in quantum computing.
The algorithm at the center of the “quantum machine learning” mini-revolution is called HHL , after my colleagues Aram Harrow, Avinatan Hassidim, and Seth Lloyd, who invented it in 2008. Many of the subsequent quantum learning algorithms extend HHL or use it as a subroutine, so it’s important to understand HHL first.
The HHL algorithm “solves Ax = b in logarithmic time,” but it does so only with the following four caveats, each of which can be crucial in practice.
1. The vector b = (b1, . . . , bn) somehow needs to be loaded quickly into the quantum computer’s memory
2. The quantum computer also needs to be able to apply unitary transformations of the form e^−iAt, for various values of t.
3. The matrix A needs to be not merely invertible, but robustly invertible, or “well-conditioned.”
4. The limitation noted earlier—that even writing down the solution vector x = (x1, . . . , xn) already requires n steps—also applies in the quantum world. When HHL is finished, its output is not x itself, but rather a quantum state |xi of log2 n qubits, which (approximately) encodes the entries of x in its amplitudes.
HHL is not exactly an algorithm for solving a system of linear equations in logarithmic time. Rather, it’s an algorithm for approximately preparing a quantum superposition.
HHL algorithm still be useful for something? Absolutely—as long as one can address all the caveats, and explain why they’re not fatal for one’s desired application. To put it differently, perhaps the best way to see HHL is as a template for other quantum algorithms.
How excited should we be about the new quantum machine learning algorithms? To whatever extent we care about quantum computing at all, I’d say we should be excited indeed: HHL and its offshoots represent real advances in the theory of quantum algorithms, and in a world with quantum computers, they’d probably find practical uses.
The new algorithms provide a general template, showing how quantum computers might be used to provide exponential speedups for central problems like clustering, pattern-matching, and principal component analysis.
In summary, they have performed the first experimental demonstration of machine learning on a photonic quantum computer. Our work demonstrates that the manipulation of high-dimensional vectors and the estimation of the distance and inner product between vectors, a ubiquitous task in machine learning, can be naturally done with quantum computers, thus proved the suitability and potential power of quantum machine learning. The ability of manipulating large vectors—combined with previously realized methods for solving systems of linear equations and Hamiltonian simulation—on quantum computers, may provide a useful quantum toolkit for dealing with the “big data”.
Theoretical prediction (a) and experimental results (b) for classifying two-dimensional vectors into two clusters. The red and blue cross are reference vectors. The evaluated value of difference of the distances of each tested vector to the two reference vectors is coded as the fill color. The result of classification is coded as the edge color (blue=A, red=B). The gray line is where the distances are the same in theory. The data acquisition time is 1 sec for each vector, collecting about 10000 events. The statistical standard deviation is much smaller than the error caused by the imperfection of the entanglement state; thus, error bars are omitted.
Abstract – Quantum algorithms for supervised and unsupervised machine learning
Machine-learning tasks frequently involve problems of manipulating and classifying
large numbers of vectors in high-dimensional spaces. Classical algorithms for solving
such problems typically take time polynomial in the number of vectors and the dimension
of the space. Quantum computers are good at manipulating high-dimensional vectors in
large tensor product spaces. This paper provides supervised and unsupervised quantum
machine learning algorithms for cluster assignment and cluster finding. Quantum machine
learning can take time logarithmic in both the number of vectors and their dimension, an
exponential speed-up over classical algorithms.

Brian Wang is a Futurist Thought Leader and a popular Science blogger with 1 million readers per month. His blog Nextbigfuture.com is ranked #1 Science News Blog. It covers many disruptive technology and trends including Space, Robotics, Artificial Intelligence, Medicine, Anti-aging Biotechnology, and Nanotechnology.
Known for identifying cutting edge technologies, he is currently a Co-Founder of a startup and fundraiser for high potential early-stage companies. He is the Head of Research for Allocations for deep technology investments and an Angel Investor at Space Angels.
A frequent speaker at corporations, he has been a TEDx speaker, a Singularity University speaker and guest at numerous interviews for radio and podcasts. He is open to public speaking and advising engagements.