State-of-the-art techniques make it possible to build a spin-chain quantum simulator based on laser-trapped circular Rydberg atoms. This simulator combines the flexibility of atomic lattices and the individual atomic observable read-out typical of ion trap, together with the strong dipole-dipole interactions of Rydberg atoms. Defect-free atomic chains can be prepared by an evaporative cooling method, which finally leaves the atoms near their vibrational ground state. Evaporation also provides us with a unit-efficiency individual-spin detection. A proper microwave dressing leads to a fully tunable spin- X X Z chain Hamiltonian. Its parameters are under direct experimental control, a unique feature of this simulator. The long lifetime of the laser-trapped circular atoms, protected from spontaneous emission, makes it possible to follow the dynamics over unprecedented time intervals, in the range of 100,000 times the spin flip-flop period. Moreover, the individual detection of all spin observables makes it possible to access a wealth of interesting properties, such as entanglement properties and local entropies.
Let us stress that the techniques proposed in this paper could have a deep impact on the thriving Rydberg-atoms physics, well beyond the realization of a full-fledged quantum simulator. Many experiments are considerably hindered by the lack of trapping of the Rydberg atoms and by the spurious transfers induced by blackbody radiation. They propose here simple solutions to overcome these bottlenecks. For instance, Rydberg atoms have been shown to be ultrasensitive probes of their electromagnetic environment. Adding to these experiments the laser-trapping capability, compatible with all high-angular-momentum states, would allow the realization of extremely sensitive, well-localized probes of the local fields. Cavity quantum electrodynamics could also considerably benefit from the techniques outlined here. Rydberg-atom cavity QED experiments have been plagued by the lack of deterministic atom sources and by the fast transit of the thermal atoms across the cavities. Laser trapping allows us to straightforwardly remove these bottlenecks. One can even envision hybrid cavity QED experiments combining superconducting circuits and laser-trapped Rydberg atoms, which can be used to create a coherent interface between microwave and optical photons.
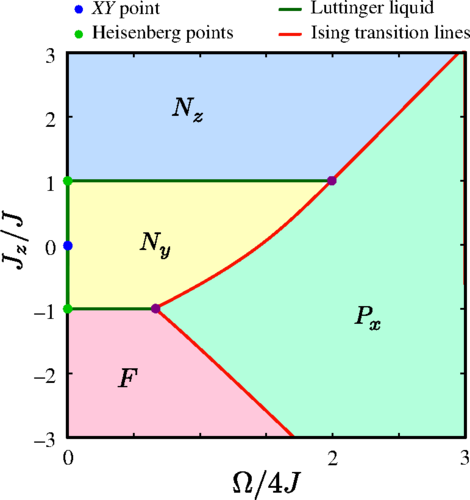
Returning to quantum simulation, a circular-state simulator with about 40 atoms could address important problems of many-body quantum physics. They have shown that slow variations of the Hamiltonian parameters make it possible to explore precisely the quantum phases of the XXZ model, generating the ground states with a high fidelity. Of course, these ground states are well known, and most of their properties can be assessed using standard numerical techniques, such as the DMRG or matrix product state (MPS) used in our extensive numerical computations. Checking the agreement between the observed phases with the expectations, we mostly assess the quality of the simulator. In particular, it would show that the residual atomic motion and other experimental imperfections have a negligible influence, as we expect.
The real interest of this simulator lies in studies of the spin-chain dynamics, which is much more demanding numerically when highly excited states or slow evolutions are at stake. For instance, fulfilling the adiabatic limit in a transition towards a gapless phase is more and more difficult when the systems size increases. A too-fast crossing of the transition line results in the generation of defects with respect to the theoretical final ground state. Exploring the generation of these defects and the limits of the adiabatic regime is particularly important in the context of adiabatic quantum computation, quantum annealing, and the Kibble-Zurek mechanism.
An essential perspective for such ground-state physics is to explore the spin-one Haldane phase using the ladder geometry. Separately prepared parallel chains could be brought into interaction with each other (by moving their Laguerre-Gauss transverse trapping beams), leading to a square ladder geometry. Using the anisotropy of the dipole-dipole interaction, the signs of the coupling between legs of a properly oriented ladder can be different. This leads to two antiferromagnetic chains that are ferromagnetically coupled. This model, in part of its phase diagram, realizes the Haldane phase. This phase possesses a nontrivial topological order, which can be straightforwardly measured in this context, and fractional spin- edge states with the open boundary conditions typical of our simulator. The ground states and low-excitation physics of the system are also well apprehended by numerical methods, but the dynamical evolution is much more difficult to simulate.
Another interesting low-energy physics problem is that of a disordered chain. Adding a laser speckle field to the optical lattice, it is fairly easy to produce random shifts of the atoms with respect to their equilibrium positions, randomly modulating the dipole-dipole interactions. In the regime, this model displays the paradigmatic competition between localization and interactions, a subject of intense activity in quantum simulation, opening the way for Bose-glass physics. Another striking feature of this model is the emergence of random singlet phases, with their unusual long-range correlations and entanglement properties in disordered systems. Remarkably, the random singlet phase of the Heisenberg point would be accessible thanks to the possibility to tune on all bonds.
The ability to rapidly modulate the Hamiltonian parameters also opens a vast realm of possibilities. Periodic modulations could be used to realize spectroscopic investigations of the elementary excitations of the system. They bear a particular interest at the critical point of the Ising transition, as shown by its remarkable integrable features, recently investigated in condensed-matter experiments. The long lifetime of the circular simulator would be instrumental in studying low-frequency excitations, not easily accessed in other contexts.
Floquet engineering corresponds to periodic variations of the couplings that are much faster than J. It allows one to design effective Hamiltonians that are not accessible with the usual control parameters. This is a particularly interesting perspective to enlarge the field of applications of the circular-state quantum simulator since all parameters of H can be easily modulated at high frequencies. In the same spirit, the proposed Rydberg setup notably makes it possible to study Floquet time crystals.
Instantaneous quenches can be realized by a sudden variation of the Hamiltonian. There is a whole range of questions on quenches that would benefit from long observation times. Whether an isolated quantum system displays equilibration and thermalization is a fundamental issue of statistical physics. As the spin-chain Hamiltonian has integrable points, one could investigate the interplay between thermalization and integrability. The intermediate relaxation times contain information on the propagation of correlations at the origin of the relaxation process. Another remarkable scenario is the prethermalization. Some observables rapidly reach a metastable steady state, while the system is not yet in its thermal equilibrium. Only a few experiments have been carried out in this regime. Finally, the dephasing time of a subsystem could be directly measured. Combining quench protocols with disordered Hamiltonians offers a way to address the issues related to many-body localization. In particular, the long simulation times would allow one to follow the logarithmic increase of the entropy that signals the many-body localization transition.
Beyond the spin-chain physics, the circular-state simulator could explore a new regime of spin-boson interactions. Shallow optical lattices lead to a situation in which the spin exchange is strongly coupled to the atomic motion. The joint motion of the atoms would then entangle with the spins, leading to a situation in which numerical simulations are far out of reach even for moderate spin numbers. In particular, the common coupling of the spin ensemble to the same bath could mimic correlated errors, which are one of the key problems for quantum error correction in quantum information protocols.
They have limited their discussions to chains with even couplings since this is the first interesting problem that this simulator could address. The use of recent atom trapping techniques could considerably extend the simulation realm. Transposing, to this context, the individually controlled multiple atomic traps on a line would allow them to individually control the position of each atom. They may thus envision preparing, from an appropriate lattice, a linear chain of circular atoms with rather large separations (10 microns or more), making interactions negligible. They could then move (in a time of the order of the trap oscillation frequency, using optimal control techniques) the atoms to put them, by pairs, in interaction for a given set of time, during which the dressing source and static field can be adjusted to provide individually controlled-pair-interaction parameters. They could use this technique, for instance, to get rid of the spurious next-nearest-neighbor coupling if it has undesired effects on the simulation. They can thus envision a simulator of a completely general spin-spin interaction model, with complete single-site addressing, both at the interaction and at the detection stage.
Finally, extensions to full 2D or even 3D geometries can also be envisioned by a mere extension to this context of recent techniques for atomic lattices and programmable optical tweezers. One could, for instance, prepare a few defect-free chains of Rydberg atoms by the van der Waals evaporation method and then pick out each atom with individual laser tweezers to finally bring them into an arbitrary spatial arrangement. The extremely long atomic lifetimes and the tight laser trapping of the circular atoms make such a scheme feasible. The techniques involved are demanding but already well established in other contexts. This dramatic extension of the proposed quantum simulator capability would allow it to address a domain where understanding the mere ground state is already quite challenging, not to mention the long-time-scale dynamics. The think there is a bright long-term future for circular-state quantum simulators.
Physical Review X – Towards Quantum Simulation with Circular Rydberg Atoms
Towards Quantum Simulation with Circular Rydberg Atoms. T. L. Nguyen, J. M. Raimond, C. Sayrin, R. Cortiñas, T. Cantat-Moltrecht, F. Assemat, I. Dotsenko, S. Gleyzes, S. Haroche, G. Roux, Th. Jolicoeur, and M. Brune
Phys. Rev. X 8, 011032 – Published 26 February 2018
The main objective of quantum simulation is an in-depth understanding of many-body physics, which is important for fundamental issues (quantum phase transitions, transport, …) and for the development of innovative materials. Analytic approaches to many-body systems are limited, and the huge size of their Hilbert space makes numerical simulations on classical computers intractable. A quantum simulator avoids these limitations by transcribing the system of interest into another, with the same dynamics but with interaction parameters under control and with experimental access to all relevant observables. Quantum simulation of spin systems is being explored with trapped ions, neutral atoms, and superconducting devices. We propose here a new paradigm for quantum simulation of spin -arrays, providing unprecedented flexibility and allowing one to explore domains beyond the reach of other platforms. It is based on laser-trapped circular Rydberg atoms. Their long intrinsic lifetimes, combined with the inhibition of their microwave spontaneous emission and their low sensitivity to collisions and photoionization, make trapping lifetimes in the minute range realistic with state-of-the-art techniques. Ultracold defect-free circular atom chains can be prepared by a variant of the evaporative cooling method. This method also leads to the detection of arbitrary spin observables with single-site resolution. The proposed simulator realizes an Hamiltonian with nearest-neighbor couplings ranging from a few to tens of kilohertz. All the model parameters can be dynamically tuned at will, making a large range of simulations accessible. The system evolution can be followed over times in the range of seconds, long enough to be relevant for ground-state adiabatic preparation and for the study of thermalization, disorder, or Floquet time crystals. The proposed platform already presents unrivaled features for quantum simulation of regular spin chains. We discuss extensions towards more general quantum simulations of interacting spin systems with full control on individual interactions.

Brian Wang is a Futurist Thought Leader and a popular Science blogger with 1 million readers per month. His blog Nextbigfuture.com is ranked #1 Science News Blog. It covers many disruptive technology and trends including Space, Robotics, Artificial Intelligence, Medicine, Anti-aging Biotechnology, and Nanotechnology.
Known for identifying cutting edge technologies, he is currently a Co-Founder of a startup and fundraiser for high potential early-stage companies. He is the Head of Research for Allocations for deep technology investments and an Angel Investor at Space Angels.
A frequent speaker at corporations, he has been a TEDx speaker, a Singularity University speaker and guest at numerous interviews for radio and podcasts. He is open to public speaking and advising engagements.