New 13 Sided and 14-Sided Shapes Can Tile Infinite Surfaces – Breakthrough in Math and Tiling

by

The recently discovered “hat” aperiodic monotile admits tilings of the plane, but none that are periodic [SMKGS23]. This polygon settles the question of whether a single shape—a closed topological disk in the plane—can tile aperiodically without any additional matching conditions
or other constraints on tile placement.

The hat is asymmetric: it is not equal to its image under any non-trivial isometry of the plane. In particular, a hat cannot be brought into perfect correspondence with its own mirror reflections. Moreover all tilings formed by copies of the hat must use both unreflected and reflected tiles. Some people have wondered whether the hat and its reflection ought to be considered two distinct shapes, thereby invalidating its status as a monotile. To some extent, this question is about tiles as physical objects rather than mathematical abstractions. A hat cut from paper or plastic can easily be turned over in three dimensions to obtain its reflection, but a glazed ceramic tile cannot.

Conclusion

Many problems in tiling theory depend implicitly or explicitly on an initial decision of when to consider two tiles in a tiling “the same”. In the Euclidean plane, if this decision is not otherwise articulated then we assume two tiles are the same if they can be brought into coincidence through any planar isometry. In this paper we first answer the einstein problem in a world where sameness is restricted to orientation-preserving isometries. The polygon Tile(1, 1) is a weakly chiral aperiodic monotile: a shape that tiles aperiodically if only translations and rotations are
permitted. Then, by modifying the edges of that polygon, we obtain a class of shapes called Spectres, which are strictly chiral aperiodic monotiles: they tile aperiodically using tiles of a single handedness, even when reflections are allowed.

Other variations of the einstein problem can be posed in which tiles are restricted to images under any given group of isometries. Each such problem comes in weak and strict forms, as above. In the weak case, we ask whether a shape’s tilings are non-periodic if tilings are restricted by fiat to the given isometries, even if it would tile periodically when all isometries are allowed.

In the strict case they require that by design, a shape does not admit any tilings that use isometries outside the group.

If they restrict our attention to translations alone, then the work of Girault-Beauquier and Nivat [GBN91] and Kenyon [Ken92, Ken93, Ken96] shows that a topological disk with a tiling by translation cannot be an aperiodic monotile. However, Greenfeld and Tao [GT21, GT22] and Greenfeld and Kolountzakis [GK23] showed that translational aperiodic monotiles do exist in sufficiently high dimensions. The next simplest case is where 180◦
rotations are allowed along with translations. Schattschneider [SF88, Problem 18.E1] posed the question of whether any tile admitting such a tiling of the plane also satisfies the Conway criterion [Gar75, Sch80], implying that it must be isohedral.

This work presents a single family of strictly chiral aperiodic monotiles, which are all essentially the same up to trivial modifications of tiling edges. It would be interesting to search for other weakly chiral or strictly chiral einsteins. It would be particularly worthwhile to find (or disprove the existence of) an aperiodic monotile with bilateral reflection symmetry, a shape for which chirality becomes moot.

They showed in Lemma 2 that they can replace the 14 edges of Tile(1, 1) by suitably oriented copies of any smooth curve to construct a Spectre, provided the replacement results in a tile with a non-self-intersecting boundary. In fact, the construction works generally for C1 curves, which suffice to force the vertices of the original polygon to meet each other in tilings. However, they leave open the question of whether some other curves (e.g., piecewise-linear paths) might permit different tilings, or whether all choices of curve produce valid Spectres.

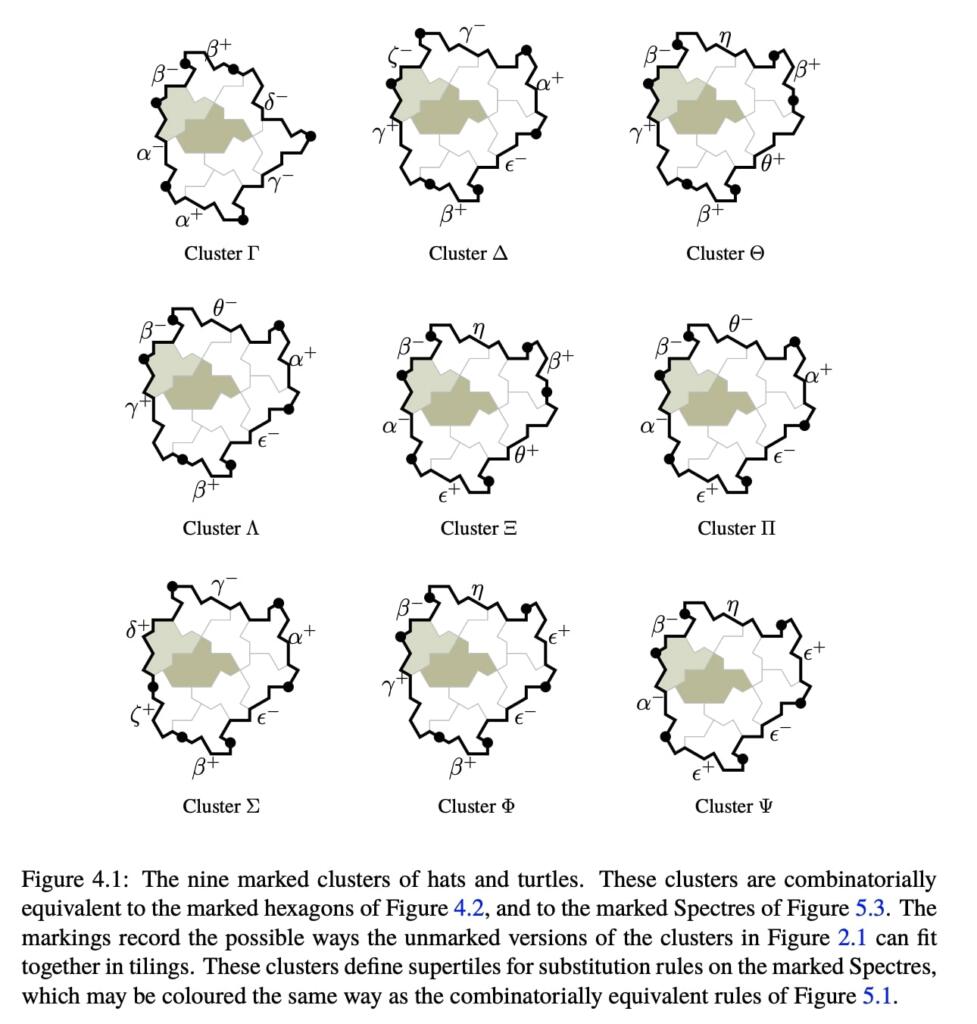
As part of their proof of aperiodicity, they derived the chiral marked hexagons of Figure 4.2.

These hexagons are meant to encode the combinatorics of clusters of Spectres, but they display interesting properties of their own that may be worthy of further study. Figure 5.2 hints at emergent patterns in tilings by marked hexagons.

Some of the hexagons of Figure 4.2 have very similar arrangements of markings; removing the distinctions between some of the edge labels can produce a smaller set of marked hexagons without reducing the set to a single trivially marked tile. In particular, combining Θ, Ξ, Φ and Ψ into a single marked hexagon, and combining Λ and Π into another marked hexagon, yields a smaller set of five marked hexagons, which preliminary computations suggest might also be aperiodic. It would be of interest to understand what small aperiodic sets of chiral marked hexagons are possible with this style of edge markings, similar to the work of Jeandel and Rao [JR21] on small aperiodic sets of Wang tiles.

7 thoughts on “New 13 Sided and 14-Sided Shapes Can Tile Infinite Surfaces – Breakthrough in Math and Tiling”

  1. An advantage for making a telescope like James Webb… Carry a stack of aperiodic tiles into space, assemble them into a mirror… and voila! you have no periodic errors caused by repeating hexagons

  3. It’s an amazing result. But if think they could make it easier to implement with a few changes to figure A.1.

    First, there should be a mystic (two tiles) above step 1, with a blue quadrilateral on the bottom half, and an arrow pointing down.

    Second, they should reflect every other step, so the tiles never reflect. That way, each step can simply add new tiles in the plane, without changing any existing tiles.

    Third, they should be more careful in choosing which Metatile in each step corresponds to everything drawn in the previous step. Figure A.1 and their example code both have the problem that it does NOT tile the plane with infinite steps. Because it only grows left/right/down from the starting tile, but never grows upward. So infinite steps will never tile the plane above the staring tile. It’s an easy fix, and they should do it.

Comments are closed.