Quantum annealing can be millions of times faster than Classical computing

Picture is the 16 qubit prototype. There was a 28 qubit prototype as well. A new announcement seems to imply 2000-4000 qubits by the end of 2008. “low thousands of qubits by the end of the year [2008]”. The die has room for a million qubits.

A research paper has results that compare the time for a quantum annealer to achieve the same levels of accuracy. They obtain times of 10 milliseconds for the quantum annealer for 10 hours of simulated annealing time–a speed-up of more than six orders of magnitude. The speed improvement in the analyzed case was 3,600,000 times.

Dwave Systems has an analog quantum computer, which should have a 2000-4000 qubit version by the end of 2008. It appears likely that they will be able to solve certain classes of optimization problems significantly faster than current methods. Optimization problems are important for businesses like Airlines and delivery companies like Fedex. If they make money solving those problems then they will have more money to research and development better versions (cleaner qubits that stay coherent longer) of their system that could solve a wider range of problems.

It is important to note that for any given problem, heuristics superior to simulated annealing almost always exist. Therefore comparing the performance benefits of quantum vs. classical annealing does not fully answer the question of what the expected speed-up of quantum annealing over the best known classical approaches is. In order to perform this analysis, more specificity with the instance class involved and the specific heuristic being used to solve the problem are required.

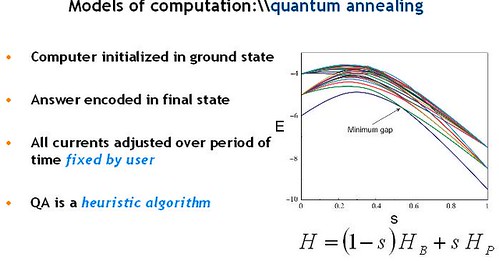
D-Wave processors are designed to harness a fundamental principle of nature that operates in both quantum that operates in both quantum and classical regimes – the propensity for all physical systems to minimize their free energy.

Free energy minimization in a classical system is often referred to as annealing. For example, in metallurgy, annealing a metal involves heating it and then cooling
it. This type of thermal annealing allows a metal that is originally filled with defects (a metastable ‘high energy’ state) to become crystalline and defect-free (the minimum free energy state).

The simulation of this type of thermal annealing using classical computers is known as simulated annealing, which is a commonly used heuristic approach to solving
certain classes of hard optimization problems.

Quantum annealing slide

Another research paper from Dwave: Quantum annealing may provide good solutions [a good approximate answer] in a short time, although finding the global minimum [perfect answer] via AQC can take an extremely long time. The energy gaps
considered here are only the avoided crossing type, which correspond to first-order quantum phase transitions. This means that only certain classes of quantum computer algorithms would work at this time.

Problems that have exponentially large number of local minima close to the global minimum, the gap becomes exponentially small making the computation time exponentially long. The quantum advantage of adiabatic quantum computation may then be accessed only via the local adiabatic evolution, which requires phase coherence throughout the evolution and knowledge of the spectrum. Such problems, therefore, are not suitable for adiabatic quantum computation.

One type of problems for which quantum mechanics may provide an advantage over classical computation is optimization. In optimization problems, one is interested in finding solutions that optimize some function subject to some constraints. Usually, not only the best solution, but also solutions close to it are of interest.

So optimization problems are ones where AQC could provide a speedup over current systems and a better useful answer.

The global scheme of adiabatic quantum computation maintains its performance even for strong decoherence. The more efficient local adiabatic computation, however, does not improve scaling of the computation time with the number of qubits n as in the decoherence-free case, although it does provide some “prefactor” improvement. The scaling improvement requires phase coherence throughout the computation, limiting the computation time and the problem size n. This means that some algorithms like the Adiabatic Grover search (faster database search) would not be sped up unless the quality of the qubits is improved beyond the level that Dwave Systems will initially be starting at.

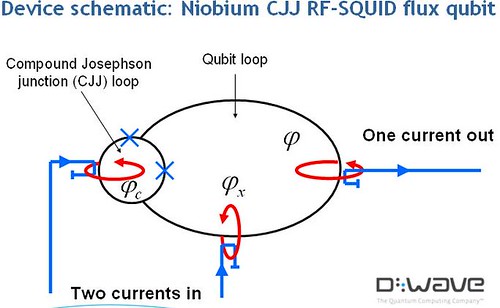
I had taken the highlights of a Dwave presentation from Nov 2007 on how their quantum computer works

FURTHER READING
More quantum computer research papers

Advertising

Trading Futures
  Nano Technology
  Netbook     Technology News
  Computer Software
    Future Predictions