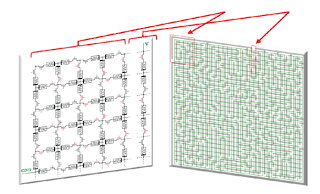
MIT Technology Review – Pershin and Di Ventra begin by creating a kind of a universal maze in the form of a grid of memristors, in other words an array in which each node is connected to another by a memristor and a switch. This can be made to represent any regular maze by switching off certain connections within the array.
Solving this maze is then simple. Simply connect a voltage across the start and finish of the maze and wait. “The current flows only along those memristors that connect the entrance and exit points,” say Pershin and Di Ventra. This changes the state of those memristors allowing them to be easily identified. The chain of these memristors is then the solution.
That’s potentially much quicker than other maze solving strategies which effectively work in series. “The maze is solved in a massively parallel way, since all memristors in the network participate simultaneously in the calculation,” they say.
They’ve tested the idea with a memristor simulator, a computer program that reproduces the behaviour of real memristors, and say it works well. And implementing the device in silicon will become easier as more development work is done in this area.
Of course, it’s not just the memristors that are doing the calculating here. Their network structure and layout is crucial too. When a maze is created, the answer is already embedded in its structure, well before any computation begins. The only question is how easily it can be extracted. This new approach, in which the entire structure of maze takes part, is clearly powerful.
This is a form of morphological computing. Think about how the human body walks or jumps. There is increasing evidence that the brain has much less involvement with this kind of movement than anybody imagined. Instead, the shape, form and material properties of bones, ligaments and muscles largely control the detail of what happens. In effect, the brain outsources control to the morphology of the system.
Arxiv – Solving mazes with memristors: a massively-parallel approach
Solving mazes is not just a fun pastime. Mazes are prototype models in graph theory, topology, robotics, traffic optimization, psychology, and in many other areas of science and technology. However, when maze complexity increases their solution becomes cumbersome and very time consuming. Here, we show that a network of memristors – resistors with memory – can solve such a non-trivial problem quite easily. In particular, maze solving by the network of memristors occurs in a massively parallel fashion since all memristors in the network participate simultaneously in the calculation. The result of the calculation is then recorded into the memristors’ states, and can be used and/or recovered at a later time. Furthermore, the network of memristors finds all possible solutions in multiple-solution mazes, and sorts out the solution paths according to their length. Our results demonstrate not only the first application of memristive networks to the field of massively-parallel computing, but also a novel algorithm to solve mazes which could find applications in different research fields.
In conclusion we have shown how a network of memristors – a memristor processor – can
solve mazes in a massively-parallel way. This approach can be realized experimentally with available systems and devices, or simply implemented on a computer. The resulting algorithm is superior to any existing maze solving methods and therefore it is ideal when the complexity of the maze increases with increasing local connectivity of the graph. We thus envision its use in a large set of applications in both basic science and technology.
If you liked this article, please give it a quick review on ycombinator or StumbleUpon. Thanks

Brian Wang is a Futurist Thought Leader and a popular Science blogger with 1 million readers per month. His blog Nextbigfuture.com is ranked #1 Science News Blog. It covers many disruptive technology and trends including Space, Robotics, Artificial Intelligence, Medicine, Anti-aging Biotechnology, and Nanotechnology.
Known for identifying cutting edge technologies, he is currently a Co-Founder of a startup and fundraiser for high potential early-stage companies. He is the Head of Research for Allocations for deep technology investments and an Angel Investor at Space Angels.
A frequent speaker at corporations, he has been a TEDx speaker, a Singularity University speaker and guest at numerous interviews for radio and podcasts. He is open to public speaking and advising engagements.