Technology Review – Jie Zou et al at the University of Florida have carved a single device out of silicon that is capable of measuring the Casimir force between a pair of parallel silicon beams, the first on-chip device capable of doing this.
There are other forces at play here too, such as residual electrostatic forces. When Zou and co take these into account, their results more or less exactly match theoretical predictions for the Casimir force that beams of this shape should generate.
The device solves a number of problems. First, because both silicon beams are made in the same lithographic step, unwanted distortions are not a significant problem. And the positioning is easier to control too since the beams and actuator are all part of the same device and so need far less calibrating and alignment. Finally, there are the measurements themselves which are more straightforward to do on a single chip than in previous experiments.
All this adds up to a significant step forward. What these guys have built is the first on-chip machine that exploits the Casimir force generated by a specific geometric configuration.
Arxiv – Geometry-dependent Casimir forces on a silicon chip (11 pages)
We report measurements of the Casimir force gradient between two parallel silicon beams with near-square cross sections at separations down to 260 nm. Both the force-sensing element and the actuator that controls the distance are integrated on the same substrate, with no need for manual alignment. Taking residual electrostatic forces into consideration, the measured Casimir force gradient agrees with the theoretical calculation based on the exact geometry. This scheme opens the possibility of tailoring the Casimir force using lithographically defined components of non-conventional shapes.
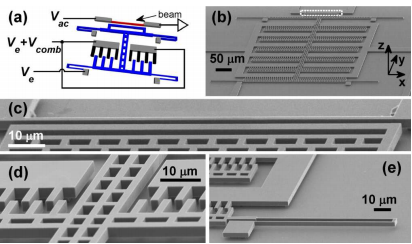
The set-up of the experiment and device. (a) A simplified schematic (not to scale) of the beam, movable electrode and comb actuator supported by four springs, with electrical connections. The current amplifier provides a virtual ground to the right end of the beam. The suspended and anchored parts of the comb actuator are shown in dark and light colors respectively. The separation d between the beam and the movable electrode was controllably reduced so that the Casimir force can be detected. (b)-(e) Scanning electron micrographs of the entire micromechanical structure (b) and close-ups of: the doubly clamped beam (c), zoomed into the white dashed box in (b); the comb actuator (d) and the serpentine spring (e).
The great promise of all this is that other shapes should be possible to manufacture too. “This scheme opens the possibility of tailoring the Casimir force using lithographically defined components of non-conventional shapes,” say Zou and co.
So instead of being hindered by uncontrollable Casimir forces, the next generation of microelectromechanical devices should be able to exploit them, perhaps to make stictionless bearings, springs and even actuators.
Exciting times for micro and nano machines.
The Casimir force gradient between a beam and an electrode with near-square cross sections has not been measured experimentally before. This configuration opens the possibility of testing a number of fundamental concepts. One important question is the validity of the PFA. The inset of Fig. 3(a)
FIG. 3. (color online) Measured Casimir force gradient F′c between the beam and the movable electrode as a function of separation d. (a) The thick solid line represents the calculated Casimir force gradients between an electrode and a beam made of silicon. The thin dashed line includes possible contributions from patch potentials. Inset: The ratios of the calculated Casimir force between the beam and the electrode to the forces given by the PFA are plotted as the thick (with substrate) and thin lines (without substrate). (b) Deviations of the measured force gradient from the dash line in (a).
compares the Casimir force gradient generated by the PFA to calculations of the exact geometry of the silicon structures. The ratio decreases with distance, reaching 56% at 6 μm. Secondly, this geometry could offer a direct demonstration of the non-pairwise nature of the Casimir force. The inset of Fig. 3(a) shows that the calculated Casimir force between the beam and the electrode depends on the presence of a third body, the substrate. When the substrate is removed, the Casimir force increases by 14% at 6 μm. Recent theoretical analysis also predicted that the Casimir force between the beams exhibits a non-monotonic dependence on the distance to the substrate that cannot be explained by pairwise additive models of the force. Since the Casimir force gradient at these distances is beyond the reach of the current setup, future experiments to reveal the aforementioned effects would require more sophisticated measurement circuitry or other detection schemes to improve the sensitivity at large (over 2 μm) separations.
If you liked this article, please give it a quick review on ycombinator or StumbleUpon. Thanks

Brian Wang is a Futurist Thought Leader and a popular Science blogger with 1 million readers per month. His blog Nextbigfuture.com is ranked #1 Science News Blog. It covers many disruptive technology and trends including Space, Robotics, Artificial Intelligence, Medicine, Anti-aging Biotechnology, and Nanotechnology.
Known for identifying cutting edge technologies, he is currently a Co-Founder of a startup and fundraiser for high potential early-stage companies. He is the Head of Research for Allocations for deep technology investments and an Angel Investor at Space Angels.
A frequent speaker at corporations, he has been a TEDx speaker, a Singularity University speaker and guest at numerous interviews for radio and podcasts. He is open to public speaking and advising engagements.